Simple equation
Simple equation
An equation of the first degree is a mathematical equality with one or more unknowns . These unknowns must be cleared or solved to find the numerical value of the equality.
Equations of the first degree receive this name because their variables (unknowns) are raised to the first power (X 1 ) , which is usually represented only by an X.
Similarly, the degree of the equation indicates the number of possible solutions. Therefore, an equation of the first degree (also called a linear equation) has only one solution.
First degree equation with one unknown
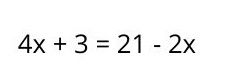
To solve linear equations with one unknown, some steps must be performed:
1. Group the terms with X to the first member and those without X to the second member. It is important to remember that when a term passes to the other side of equality, its sign changes (if it is positive it becomes negative and vice versa).
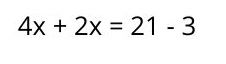
3. The respective operations are performed on each member of the equation. In this case, an addition corresponds to one of the members and a subtraction to the other, which results in:
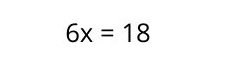
4. Solve for X , passing the term in front of it to the other side of the equation, with the opposite sign. In this case, the term is multiplying, so now move on to dividing.

5. Solve the operation to know the value of X.
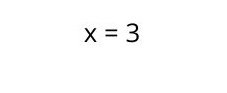
Then, the resolution of the first degree equation would be as follows:
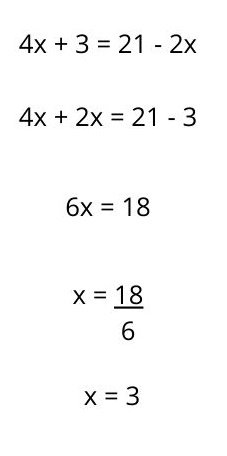
First degree equation with parentheses
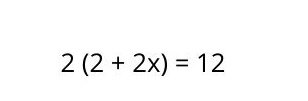
In a linear equation with parentheses, these signs tell us that everything inside them must be multiplied by the number in front of them. This is the step by step to solve equations of this type:
1. Multiply the term by everything that is inside the parentheses , with which the equation would be as follows:
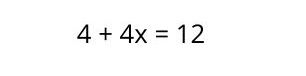
2. Once the multiplication has been solved, there remains a first degree equation with one unknown , which is solved as we have seen previously, that is, by grouping the terms and doing the respective operations, changing the signs of those terms that pass to the other side of equality:
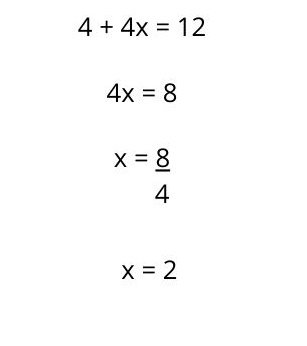
First degree equation with fractions and parentheses
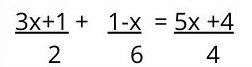
Although first-degree equations with fractions seem complicated, they actually only take a few extra steps before they become a basic equation:
1. First, we must obtain the least common multiple of the denominators (the smallest multiple that is common to all the denominators present). In this case, the least common multiple is 12.
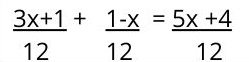
2. Then divide the common denominator by each of the original denominators . The resulting product will multiply the numerator of each fraction, which are now in parentheses.
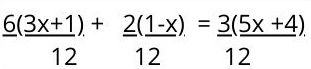
3. The products are multiplied by each one of the terms that are inside the parentheses , as it would be done in a first degree equation with parentheses.
Upon completion, we proceed to simplify the equation by eliminating the common denominators:
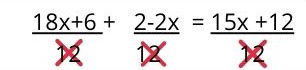
The result is an equation of the first degree with one unknown, which is solved in the usual way:
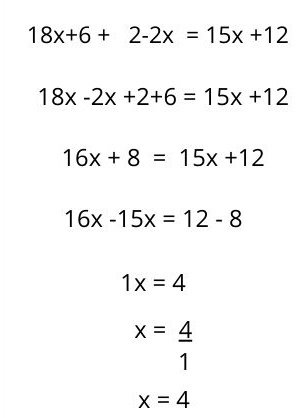
- Update date: March 7, 2021.
Recommended Contents
.
.